Students preparing for the BECE are encouraged to take a,look at the Sample 2024 BECE Mathematics Questions and Answers shared here.
Sample 2024 BECE Mathematics Questions and Answers
PAPER 2-ANSWER ALL QUESTIONS [60MARKS]
(a) There is a contest where contestants were given the digits
The winner of the contest formed a number from the digits, it starts with odd digit, the hundred position is even digit and the last digit is an even digit but greater than the hundred position digit. He used the digits once. Write the number
The second winner formed a number from the digits; the thousand position is the greatest even digit, the tens position is greater than the hundred but all even and the last digit is an old number. He used the digits once. Find the number
(b) (i) Evaluate √50 +√98 -√75 +√147 leaving the answer in the form a√x +b√y
(ii) Rationalise (2√7)/√3
(c). The VAT rate of Ghana is 12.5%. A man bought an item at GH₵ 4500.00, VAT inclusive.
Calculate:
(i) the basic cost of the item.
(ii) the VAT paid by the man.
2. (a). The NHIL inclusive price of a television set is GH₵1200.00. If the NHIL is charged at a rate of 2.5%,
Find
the cost of the television set (NHIL exclusive).
the NHIL charged.
(b). The diagram below represents a triangle
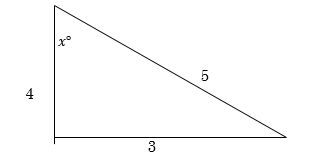
find sinx and cosx
find the angle x
(c). Simplify (2/5÷4/15)+(1/25÷2/15)
3. Using ruler and a pair of compasses only
Construct
Line AB = 8cm
A perpendicular at A and B
Line CD parallel equal to AB where BC : AD = 1: 1 = 8cm
b. Construct the mediators of AB and BC, name O the point of intersection
With O as the centre and radius OA, draw a circle.
Shade figure ABCD. What shape is ABCD.
c. Calculate the are total area of the figure
4. (a)(i) The midpoint of point of A and B is M(3, 4). The coordinates of A and B are (2, a) and (b, 12) respectively. Find the values of a and b.
(ii) Find the value of x in the equation; 1/27=9^(x-2)
(b). An isosceles triangle has equal sides, 6cm long and a base of 4cm long. Find the altitude of the triangle.
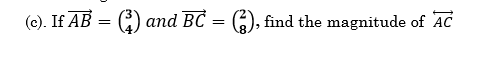
5. (a) Kojo says his taxi makes a number of trips each day as shown in the table below:
| Days | Mon | Tue | Wed | Thurs | Fri | Sat | Sun |
| Trips | 8 | 6 | 10 | 10 | 9 | 10 | 3 |
Calculate the mean, median and mode for Kojo’s trips for the week
Which measure of central tendency best represents or describes the number of trips that Kojo makes each day? Justify the choice of central tendency in(ii)
(b) A box contains 3 blue pens and 4 pink pens. A pen is taken from the box, its colour noted, and then replaced. Another pen is taken and its colour noted.
i. What is the sample space of the 1st and the 2nd trials?
ii. Draw a probability tree diagram to represent the event.
6. (a) The sum of three consecutive odd numbers is/are 39. Find the numbers
Given that the coordinates of the distance between A and B are (6,6) and (3,2)
Find the gradient of AB
Find the length of the distance between A and B
The ratio of the sides of a triangle are 2:1:2. If the average side of the triangle is 40cm
Calculate each side of the triangle
Show that, the triangle is an isosceles
Sample 2024 BECE Mathematics Questions and Answers EDUCATION-NEWS CONSULT
MATHEMATICS
MARKING SCHEME
QUESTION 1a.
8, 9, 4, 5
The number = 9648 or 9468 A2
The number =8469 A2 =4MARKS
QUESTION 1b(i)
√50 +√98 -√75 +√147
=√(2×25) +√(2×49) -√(3×25) +√(3×49) M1
=5√2 +7√2 -5√3 +7√3 B1
=9√2+2√3 A1 = 3MARKS
QUESTION 1b(ii)
(2√7)/√3
=(2√7)/√3 ×√3/√3 M ½
=(2√(7×3))/〖√3〗^2 B1
=(2√21)/3 or 2/3 √21 A ½ =2MARKS
QUESTION 1c(i)
VAT rate = 12.5%
Cost = GH₵4500.00 VAT inclusive
Cost VAT inclusive = cost + VAT of cost B 1
Let the cost = 100%
Cost VAT inclusive = (100+12.5)% = 112.5% M ½
112.5 = 4500
100. = x M ½
112.5x=4500×100 B ½
112.5/112.5 x=(4500×100)/112.5 B ½
x=GH₵4000.00 A1 =4MARKS
QUESTION 1c(ii)
The VAT paid = 4500-4000 M1
The VAT paid = GH₵500.00 A1=2MARKS
QUESTION 2(a) (i)
NHIL inclusive = GH₵1200.00
NHIL charge = 2.5%
Let cost of TV = 100%
Cost inclusive = 102.5% M ½
102.5 = 1200
100 = x B ½
102.5x=1200×100 M ½
x=(1200×100)/102.5 M ½
x=1170.732 or 1170 A1= 3MARKS
QUESTION 2(a)(ii)
The NHIL charged = 1200-1170.732 M1
The NHIL charged = GH₵29.268 A1 =2MARKS
QUESTION 2(b)
sin〖x=〗 3/5 A1
cos〖x=4/5〗 A1 = 2MARKS
sin〖x=3/5〗 M 1
〖x=sin〗^(-1)(3/5) M 1
x=36.87° M 1 = 3MARKS
QUESTION 2(c)
(2/5÷4/15)+(1/25÷2/15)
=(2/5×15/4)+(1/25×15/2) M ½
=((2×15)/(5×4))+((1×15)/(25×2)) M ½
=3/2+3/10 B ½
=(3(5)+3(1))/10 B ½
=(15+3)/10 M 1
=18/10 M 1
=1 4/5 A 1 = 5MARKS
QUESTION 3
Marking
AB = B1
Perpendicular at B =B1
Perpendicular at A =B1
Parallel line CD = B1
Bisector of AB = B1
Bisector of BC = B1
Naming intersection O = B 1
Circle with radius OA = B2
Shading ABCD = B 1 = 10marks
(c) Area of the total shape = area of circle – area of square M1
Radius = 5.5cm B1
Total area = 5.5×5.5×3.142-8×8 M1
Total area = 95.0455-64 M1
Total area =31.0455〖cm〗^2 A1= 5MARKS
QUESTION 4
(i) Mid-point (3, 4), A(2, a) and B(b, 12)
(3,4)=((2+b)/2,(a+12)/2) B ½
3=(2+b)/2 M ½
6=2+b
6-2=b
b=4 A ½
4=(a+12)/2 B ½
4(2)=a+12
8=a+12 M ½
8-12=a
a= -4 A ½ =3MARKS
1/27=9^(x-2)
3^(-3)=3^(2(x-2)) B ½
-3=2(x-2)
-3=2x-4 M ½
-3+4=2x
1=2x
1/2=2x/2 M ½
x=1/2 A ½ = 2MARKS
QUESTION 4b
H^2=2^2+6^2 M1
H^2=4+36 B1
H=√40 M1
H=6.234cm A2 =5MARKS
QUESTION 4C
If (AB) ⃗=(3¦4) and (BC) ⃗=(2¦8),
(AC) ⃡+ (BC) ⃗ =(AC) ⃗ M ½
(3¦4)+(2¦8) = (AC) ⃗ B ½
((3+2)¦(4+8)) =(AC) ⃗ M ½
(5¦12) =(AC) ⃗ M ½
(AC) ⃗=√(5^2+〖12〗^2 )
(AC) ⃗=√(25+144) B1
(AC) ⃗=√169 B1
(AC) ⃗=13 A1 =5MARKS
QUESTION 5a.
Days Monday Tuesday Wednesday Thursday Friday Saturday Sunday
Trips 8 6 10 10 9 10 3
Mean = (∑▒x)/n M1
Mean =(8+6+10+10+9+10+3)/7 M1
Mean = 56/7 B1
Mean = 8 A1
Median = 28th and 29th position M1
Median = Thursday A1
Mode = Wednesday, Thursday, Saturday A2
Mean . Mean is the average which represents true number of trips A2
QUESTION 5bi
{BB, BP, PB, PP} sample space for 1st and 2nd trial A2
QUESTION 5b(ii) A3
QUESTION 6
Let the first number be x
Common difference = 2
So they are ; x, x+2, x+4 ______B1
Sum = 39 ______B1/2
x + (x+ 2 ) + (x + 4) = 39 ______M1/2
x + x + x+ 2 + 4 = 39
3x +6 = 39 ______M1/2
3x = 39 – 6 ______M1/2
3x = 33 _____B1/2
=3x/3 = 33/3 _______B 1/2
x= 11 _____A1
The numbers are 11, 13, 15
A (6,6) B (3,2)
Gradient = (y2-y1)/(x2-x1) ______ B1/2
Gradient(M) = (2-6)/(3-6) _____M1
Gradient = (-4)/(-3) ______M 1/2
Gradient = 4/3 ______A1
Length AB = √(∆x^2+∆y^2 )________________________B 1/2
AB = √((6-3)^2+〖(6-2)〗^2 ) _______M1/2
= √(3^2+4^(2 ) ) ______M1/2
= √(9+16) ______B1/2
= √25 _____M1/2
/AB/ = 5units
QUESTION 6c
Sides = 3
Ratio = 2 : 1 : 2
Total ratio = 2 + 1 + 2 =5
Average side = 40cm ………………………………………………………B 1/2
Average = (Total ( perimeter))/(number of sides) …………………………………………………………M1/2
40 = p/3 ……………………………………………………………M1/2
Perimeter = 3×40 ……………………………………………………………B1/2
Perimeter = 120cm = total ……………………………………………………………A1/2
Sides = A = 2/5 × 120 = 48cm
B = 1/(5 ) ×120=24cm
C =2/5 ×120 = 48cm ……………………………………………………………A11/2
(ii) The triangle is an isosceles if two sides are equal
A = 48cm
B =24cm
C = 48cm
A = C, therefore the triangle is an isosceles ………………………A
We hope these Sample 2024 BECE Mathematics Questions and Answers help you revise.
Leave a Reply